ミクロ経済学基礎
2.1 予算制約に基づく個々人の判断
この節の最後には、以下のことができるようになります。
- 予算制約を計算・グラフ化する
- 機会集合と機会費用について説明する
- 限界効用逓減の法則を評価する
- 限界分析と効用が選択にどのような影響を与えるかを説明する
典型的な消費者の予算問題を考えてみましょう。消費者の欲しいものや必要なものに使える金額は総収入によって制限されています。たとえばAlphonsoさんの場合、1週間で使えるお金は10ドルで、それを通勤のためのバスのチケット代とランチに食べるハンバーガー代に割当てる必要があるとします。バスのチケット代は1回50セントでランチに食べるハンバーガー代は1回2ドルです。Alphonsoさんの予算問題は図2.2の通りです。
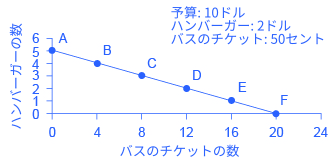
図2.2 予算制約:Alphonsoさんの予算制約線予算制約線上の点はハンバーガーとバスのチケットの組み合わせの合計がAlphonsoさんの予算10ドルになる点を表します。予算制約線の傾きはハンバーガーとバスのチケットの相対価格によって決定されます。購買可能領域(予算集合)の中で、1つのハンバーガーをあきらめることは4枚のバスのチケットを手に入れることを意味します。
グラフの縦軸はハンバーガーの購入数を、横軸はバスのチケットの購入数を示しています。もしAlphonsoさんが所持金の全てをハンバーガーに充てると、彼は1週間に5つ買うことができます(1週間あたり所得10ドル/ハンバーガー1個当たり2ドル=1週間あたり5個のハンバーガー)。しかし、もしそのように行動すると、彼はバスのチケットを購入することができなくなるでしょう。図の点Aはこの選択を表しています。代わりに、もしAlphonsoさんが所持金の全てをバスのチケットに充てると、彼は1週間に20枚買うことができます(1週間あたり所得10ドル/チケット1枚当たり0.5ドル=1週間あたり20枚のバスのチケット)。しかし、その際に彼はハンバーガーを購入することができません。点Fはこの選択を表しています。
もし我々がAF間の全ての点を繋ぐと、Alphonsoさんの予算制約線を導くことができます。この線は2つの財の価格と予算額から、彼がハンバーガーとバスのチケットを買うことができる選択肢の全てを示しています。
もしAlphonsoさんが多くの人々のようであれば、彼はバスのチケットとハンバーガー両方を含んだ選択肢を選ぶでしょう。それは彼が予算制約線の点Aと点F間の選択肢を選ぶということです。その制約線上(もしくは制約線内)の全ての点では彼が買うことができるハンバーガーとバスのチケットの組み合わせを示しています。制約線外の数量は彼の予算以上のお金を必要とする為、どこであっても得ることができません。
この予算の制約は、ハンバーガーとバスのチケットのどちらかを選ぶ際にAlphonsoさんが直面するトレードオフを明らかに示しています。彼は現在点D、つまり12枚のバスのチケットと2つのハンバーガーを買う余裕があると考えてください。Alphonsoさんがもう一つのハンバーガーを買うのに、どれくらいの費用がかかるでしょうか。2ドルと答えるのが自然ですが、経済学者は異なった考え方をします。経済学者は、問を次のように言い換えます:「予算の範囲内で、Alphonsoさんはもう一つのハンバーガーを手に入れるために何枚のバスのチケットを諦めなければならないでしょうか」。バスのチケットは50セントかかるので、Alphonsoさんはもう一つのハンバーガーを買うために4枚のバスのチケットを諦めなければなりません。これがAlphonsoさんが支払う本来の費用です。
機会費用の考え方
何かを得るためにあきらめなければならない状況を説明するために経済学者は機会費用という用語を使います。機会費用の裏にある考えは、あるモノの費用は、何か他のことをする、あるいは、何か他のものを購入するための失われた機会であるというということです。要するに、機会費用は2番目に良い選択肢の価値なのです。Alphonsoさんにとって、ハンバーガーの機会費用は、彼が諦めなければならないであろう4枚のバスのチケットのことです。彼は、ハンバーガーの価値が、もう一つの選択肢―この場合だとバスのチケットの価値を上回るかどうかによってハンバーガーを選ぶべきかどうか決めるでしょう。人々はより欲しいと思っている何かのために、何かを諦めなければならないというトレードオフに必然的に直面します。
こちらのサイトでは、自分の代わりに他の誰かにお金を支払って列に並んでもらうという機会費用の具体例を見ることができます。
経済学における基本的な原則は、全ての選択は機会費用を持つということです。例えばあなたが経済学の授業中に寝るとすると、その機会費用は授業を聞かなかったことによって逃した学びです。もしあなたが収入をビデオゲームに費やすならば、あなたは映画にそのお金を費やすことはできません。もしあなたがひとりの人と結婚するなら、あなたはそれ以外の誰かと結婚する機会を諦めることになります。要するに、機会費用は私たちの身の回りにあり、人間の存在の一部なのです。
次の「予算制約の理解」では、予算制約の計算における段階的な分析を示しています。それを読んで、補論「経済の原理における数学の利用」でさらに説明するもう一つの重要なコンセプトである傾斜について理解しましょう。
予算制約の理解
ほんの少しの数学を用いることで、予算制約についての理解が容易になります。補論「経済原理における数学の利用」では、このテキストの中で必要になる全ての数学が説明されています。もしも数学がそこまで得意ではないのなら、補論を確認することをおすすめします。
ステップ1:任意の予算制約線は以下の式で表されます。
$$ 予算 = P_{1} \times Q_{1} + P_{2} \times Q_{2} $$
ここでは、 \(P\) は財の価格、 \(Q\) は財の量を表し、 \(予算\) は支払われる収入を表します。
ステップ2:予算制約式をシナリオに当てはめます。Alphonsoさんの場合どのように働くのかを以下でみてみます。
$$ 予算 = P_{1} \times Q_{1} + P_{2} \times Q_{2} $$ $$ \begin{align} 予算\$10 = & ハンバーガー1個当たり\$2 \times ハンバーガーの個数 \\ & + バスのチケット1枚当たり\$0.50 \times バスのチケットの枚数 \end{align} $$ $$ \$10 = \$2 \times Q_{ハンバーガーの個数} + \$0.50 \times Q_{バスのチケットの枚数} $$
ステップ3:ほんの少し代数を用いることで、この式を1次式に変換できます。
$$ y = b + mx $$
Alphonsoさんの場合は、以下のように式を変形していきます;
$$ \$10 = \$2 \times Q_{ハンバーガーの個数} + \$0.50 \times Q_{バスのチケットの枚数} $$
ステップ4:式を単純化します。まずは式の両辺に2をかけましょう。
$$ \begin{align} 2 \times & 10 = 2 \times 2 \times Q_{ハンバーガーの個数} + 2 \times 0.5 \times Q_{バスのチケットの枚数} \\ & 20 = 4 \times Q_{ハンバーガーの個数} +1 \times Q_{バスのチケットの枚数} \end{align} $$
ステップ5:両辺から\( 1 \times Q_{バスのチケットの枚数} \)を引きましょう。
$$ 20 – Q_{バスのチケットの枚数} = 4 \times Q_{ハンバーガーの個数} $$
両辺を4で割ります。
$$ \begin{align} 5 - 0.25 \times Q_{バスのチケットの枚数} & = Q_{ハンバーガーの個数} \\ & or \\ Q_{ハンバーガーの個数} & = 5 - 0.25 \times Q_{バスのチケットの枚数} \end{align} $$
ステップ6:この式は図2.2における予算制約線と一致します。式で表されている通り、切片が5で傾きが-0.25です。\( Q_{バスのチケットの枚数} \)に20枚という数字を代入すると、ハンバーガーが0個得られると分かります。\( Q_{バスのチケットの枚数} \)に別の数字を代入すると、別の結果が得られます。表2.1は予算制約線上にとれる点を表しています。
| 点 | ハンバーガーの個数(1個2ドル) | バスのチケットの枚数(1枚50セント) |
|---|---|---|
| A | 5 | 0 |
| B | 4 | 4 |
| C | 3 | 8 |
| D | 2 | 12 |
| E | 1 | 16 |
| F | 0 | 20 |
表 2.1
ステップ7. 予算制約の傾きは常に、横軸にある財の機会費用を表しています。アルフォンゾにとって傾きは-0.25で、バスのチケットを買うたびにハンバーガーの1/4をあきらめなければならないことを意味しています。言い換えれば、チケットを4つ買うたびにアルフォンゾは一つのハンバーガーをあきらめる必要があります。
ここには二つの大事なポイントがあります。まず一つ目に、傾きの符号はマイナスの値となっています。これは、片方の財を手に入れるためにはもう片方の財のいくらかをあきらめる必要があるということです。二つ目のポイントとして、傾きを、バスのチケットの価格(グラフの横軸にある財)をハンバーガーの価格(グラフの縦軸にある財)で割った値として定義します。この場合は$0.50/$2 = 0.25 です。それら2つの価格を割ることで機会費用を素早く導くことができます。
機会費用を明らかにする
機会費用を価格として考えることが合理的である場合も多いです。ある人が新しい自転車を300ドルで買ったとすると、その300ドルは犠牲となった「他方の消費」の価格と釣り合います。実生活においては特定の代替物を考える必要はないかもしれません。また、機会費用を正確に把握したい場合、価格による指標は正確ではない場合があります。この問題は時間というコストが含まれる場合特に顕著に現れます。
例えば、ある上司が「チーム意識を育む」という目的のために従業員全員に2日間の休養を設けたとします。目に見える費用としては、休養を実現するため外部のコンサルティング会社への相談のための費用や、参加者全員のための部屋代や食事代があります。しかしここにさらに「休養の二日間は従業員は仕事をしない」という機会費用も存在しています。
大学に通うことも、機会費用が目に見える費用よりも高くなる例の一つです。大学に通うことにより発生する金銭的な費用として授業料、教科書代、参考書代、家賃、食費などがあります。これに加え、授業に出席している時間や勉強している時間は仕事をすることはできません。このため、大学に通うということは目に見える費用と、稼ぐことができた収入という機会費用が生じます。
飛行場のセキュリティ強化にはどのような機会費用が存在するか
2001年9月11日のアメリカ同時多発テロ事件の後、旅の安全性を高めるための複数の手段が提案されました。一般の乗客に扮れて「スカイマーシャル」と呼ばれる武装警察官をを搭乗させるというのもその一つです。すべてのフライトにスカイマーシャルを配備するにはおおよそ30億ドルかかると試算されます。またあるいは、テロリストが飛行機をハイジャックするのを困難にするためにアメリカにあるすべての機体のコックピットのドアを強化するには4.5億ドルかかると試算されます。さらに、手荷物を3Dスキャンする装置や顔認証機能を搭載したカメラといった、より高度な技術を使用したセキュリティ設備を購入するには20億ドルかかると試算されます。
しかし、航空のセキュリティ強化で最も大きい費用はお金がかかるものではなく、飛行場での待ち時間による機会費用です。アメリカ合衆国運輸省(DOT)によると、2015年には国内便及び国際便合わせて8億9550万人の予定旅客がいました。2001年の同時多発テロ以来セキュリティ審査はより厳しくなり、その結果以前よりも審査にかかる時間が長くなっています。例えば、平均で旅客一人あたり30分長くなっていたとしましょう。経済学者は多くの場合、時間による機会費用を金銭的なものに変換するために、時間に価格をあてはめます。飛行機を利用する人の多くは収入の多いビジネス関係者であるため、控えめに見積もって旅客にとって1時間は20ドルに相当するとします。大雑把な計算をすると、飛行場での待ち時間により年間 8億人 × 0.5時間 × 20ドル/時間 = 80億ドル もの機会費用が生じている計算になります。待ち時間に寄る機会費用は直接的な支払いが行われる費用と同じくらい重要であることがわかります。
場合によっては、機会コストを意識することは行動を変える可能性があります。例えば、あなたが毎日職場で昼食に8ドルを使うと想定してください。あなたは、家から昼食を持ってくることで1日あたりたったの3ドルしかかからないということをよく知っているとしましょう。ですから、各日、レストランで昼食を買うことの機会費用は5ドルです(つまり、昼食を買うための費用8ドルから家から持ってきた昼食の費用3ドルを引いたものが費用としてかかるということ)。毎日の5ドルはそんなに多くないように思えます。しかしながら、もし1年間毎日レストランで昼食をとった場合を見積もると1年250日×各日5ドルで1,250ドルとなります。ちゃんとした旅行1回分の費用と等しいのです。もし機会費用を「1日あたり5ドル」ではなく「素敵な休暇」と表現するならば、あなたは異なる選択をするかもしれません。
限界意思決定と限界効用逓減
予算制約の枠組みは、現実世界の大部分の選択が、あるもののすべて、あるいは他のものすべてを得ることに関するものではないということを強調するのに役立ちます。すなわち、予算制約の一端を選ぶのではありません。ほとんどの選択は、限界分析が行われます。それは、ある財を少し多く、あるいは少し少く選ぶ際の効用と費用を吟味することを意味しています。人々は自然に費用と効用を比較しますが、多くの場合、費用の合計と効用の合計をみています。しかし最善の選択を行うためには、ある選択肢から他の選択肢に移る際、費用と高効用がどのように変化するかを比較する必要があります。限界分析を「変化の分析」と考えることができます。限界分析は経済学の至るところで使われています。
効用についての考え方に移りましょう。人々は財とサービスがもたらす効用や満足感のためにそれらを求めます。消費者選択の章でみていく効用と呼ばれるものは、主観的なものではありますが、現実的なものなのです。経済学者は通常、ある財が消費されればされるほど、より効用を手に入れることができるものだと考えます。同時に、通常あるものを5回目、10回目に使用することで受ける効用よりも、最初に使用することで受ける効用のほうが大きいものです。例えば、Alphonsoさんがハンバーガーとバスのチケットにおける選択をするとき、彼が最初にバスに乗るということ選んだことが彼に大きな効用を与えることになるかもしれません。もしかしたらバスに乗ることが、彼を仕事の面接や医者の予約に間に合うのを手助けするかもしれません。しかし後々乗るバスからはあまり効用を受けられないかもしれません。バスに乗ることは雨の日に時間つぶす程度の効用になるかもしれません。同じ様に、Alphonsoさんが最初に買ったハンバーガーは、朝食を食べ忘れてとてもおなかが減っている日だったかもしれません。この場合は大きな効用を与えることになるでしょう。しかし、もしAlphonsoさんが毎日ハンバーガーを食べていたら、最後の方はかなり味に飽きてしまうかもしれません。一般的なパターンとして最初の数回の財の消費は後々の消費より高い水準の効用をもたらす傾向にあります。経済学者はこれを限界効用逓減の法則と呼んでいます。つまり、たくさんのものを受け取った時、それぞれの追加のものに与えられる追加の(または限界)効用は減少するということです。言い換えると、6枚目のピザより1枚目のピザのほうが満足感が得られるということです。
限界効用逓減の法則は人々や社会が滅多に0か100かの選択をしないことを説明します。皆さんは「私の好物はアイスクリームだからこれからはアイスクリーム以外のものは食べません」とは言わないでしょう。こう言い換えることもできます。たとえもしも好物の食べ物からとても大きい効用を得て、もしその食べ物しか食べなかったとしても、最後の食べ物から得られる追加的効用もしくは限界効用はたいして大きなものではありません。こうも言い換えられるでしょう。ほとんどの労働者が「休暇が楽しいのでこれからは仕事はしない」と言わないでしょう。労働者は休暇はとても素晴らしいことではあるけれど、全てが休暇で収入が全く無いという組み合わせはそこまで魅力的ではないことを認識しているのです。予算制約の枠組みは、希少性の世界の中で人々が選択をするときに、限界分析を使うことで、何かをちょっと多く、あるいはちょっと少なくなにかを望むかを考える、ということを示唆しています。
合理的な消費者は限界効用が機会費用を上回る際にのみ、同じ商品を再度購入します。Alphonsoさんの例では点Aから点B、点Cとさらに続いて予算制約線は下がっています。彼がバスのチケットをより多く購入するにつれて、バスのチケットの限界効用は次第に下がっていき、一方で先送りにされたハンバーガーの限界費用である機会費用は次第に増加します。最終的に機会費用は、バスのチケットの追加的な限界効用を超過するのです。Alphonsoさんが合理的ならば、ひとたび限界効用が機会費用と等しくなった場合、より多くのバスのチケットを買い求めることはないでしょう。Alphonsoさんがバスのチケットを何枚買うかを明確に言い当てることはできませんが、その枚数は彼が買うことができる最大の20枚にはならないでしょう。
埋没費用(またはサンクコスト)
予算制約の枠組みの中では、全ての決断は次に何が起こるかが関係します。例えば、今後どのくらいの量の商品を消費するか、どのくらいの時間働くか、もしくはどのくらい節約できるか、などです。これらの決断において、過去の選択を振り返ることはできません。つまり、予算制約の枠組みは埋没費用(またはサンクコスト)が現在の状況に影響を与えないと仮定しています。埋没費用とは過去に発生した、取り戻すことのできない費用のことを指します。
セリーナさんの場合を考えてみましょう、彼女は映画を見るために8ドルを払いました。しかし、映画を見始めて30分後、彼女はその映画があまりにつまらないことに気づきます。彼女はチケットの代金をせっかく支払っているのだから、そのまま座って残りの映画を見続けるべきなのでしょうか、それとも帰るべきなのでしょうか。彼女がチケットに払った代金こそが埋没費用です。その映画館の館長が同情でもしてくれない限り、セリーナさんのチケット代は返ってこないでしょう。しかし、そのまま映画を見続けるということは時間という機会費用をずっと払い続けるということを意味します。彼女はここで行動を選ぶことになります。次の90分間を酷い映画を耐え忍ぶために使うか、あるいは他に何かをするために使うか。酷い映画を耐え忍ぶ以外のことだったらもう何だって構わないかもしれませんね。埋没費用の教訓は、取り返すことのできないお金や過ぎてしまった時間については忘れて、その代わりに限界費用と、現在そして未来における有意義な選択に焦点を当てるべきだということです。
人々や企業にとって、埋没費用を考えることは苛立たしいかもしれません。それはしばしば過去の判断の誤ちを認めることを意味します。成績の振るわない新商品になかなか見切りをつけることができない企業も後を絶ちません。なぜかというと、その新商品の開発や立ち上げに企業は多くのお金を使っているからです。しかしながら、埋没費用の教訓からすると、埋没費用を無視し、未来に何が起こるのかに基づいて判断をすることです。
2つの商品のみのモデルから、複数の商品を含むモデルへ
この本の中で使われているほとんどのモデルと同様に、たった2つの商品しか含まれない予算制約図は現実的なものではありません。結局、現代の経済において人々は何千もの商品の中から選択をします。しかし、たくさんの商品を含むモデルについて考えるということは、私たちがここで議論すべきことを単純に増やすことを意味します。一本の予算制約線を書くことで、2つの商品間のトレードオフを示すことができ、複数の予算制約線を書くことができれば、多種多様な商品の組み合わせ間のトレードオフの可能性を示すことができます。経済学の上級クラスでは、購入されうるできる限り多くの財やサービスを、それらの量や価格とともに数学の方程式を用い、全ての財やサービスへの総支出が、利用可能な全ての予算に制限されることを示します。私たちがこの本の中で提示した2つの商品で描いたグラフは、あらゆる選択が機会費用を持つことをはっきりと表しており、そしてその考え方は現実世界へと持ち出されるのです。
批判的思考のための問題
- Alphonsoさんが使っているバスのチケットの料金が0.5ドルから1ドルに上がり、ハンバーガーの価格が2ドルから4ドルに上がったとします。この場合でもバスのチケットの機会費用はどうなるでしょうか。また、Alphonsoさんの予算が10ドルから20ドルに増えたとします。この場合彼の予算制約はこれら3つの要因によってどのような影響を受けるでしょうか。
対訳表
| 予算制約 | budget constraint |
| 機会費用 | opportunity cost |
| 限界分析 | marginal analysis |
| 効用 | utility |
| 限界効用逓減の法則 | law of diminishing marginal utility |
| 埋没費用、サンクコスト | sunk costs |
| 機会集合 | opportunity set |