ミクロ経済学基礎
6.1 消費選択
この節の最後には以下のことができるようになります。
- 総効用を計算する
- 効用を最大化する選択肢を挙げる
- 限界効用と限界効用逓減の重要性を説明する
アメリカ人の消費行動に関する情報はアメリカ労働省労働統計局による消費者の支出調査から手に入れることが出来ます。表6.1は、アメリカの世帯のさまざまな支出の平均を示しています。最初の行は所得を示しています。2行目は、1行目の所得から税と個人貯蓄を差し引いたものです。それを見ると2015年にはアメリカの世帯平均消費が48,109ドルであったことがわかります。この表はその消費を様々なカテゴリーに分類しています。表からわかる通り、アメリカの平均世帯の約1/3の支出は住居や家賃に向けられ、もう1/3は食料や車の費用、残りは様々なものに向けられています。この割合は世帯の収入や地理的条件や好みなど様々な要因によって変化します。
| 税引き前の世帯収入の平均 | $62,481 |
| 平均年間支出 | $48.109 |
| 家庭内での食事 | $3,264 |
| 外食 | $2,505 |
| 住宅 | $16,557 |
| 衣服とサービス | $1,700 |
| 交通費 | $7,677 |
| 医療費 | $3,157 |
| 娯楽費 | $2,504 |
| 教育費 | $1,074 |
| 保険料・年金 | $5,357 |
| その他:お酒、たばこ、本、美容、寄付金など | $3,356 |
表6.1 2015年におけるアメリカ人の消費行動 (Source: http://www.bls.gov/cex/csxann13.pdf)
総効用と限界効用逓減
経済学者は、世帯がどのような選択をするかを理解するために、消費者が何を買うことができるかを見ます。消費者が何を買うことができるかは、予算制約線と、選択から発生する総効用または満足度で表されます。予算制約線では、ある財の数量は横軸に、もう一つの財の数量は縦軸に設定します。この予算制約線は、消費者の所得の範囲内で購入可能な二つの財の様々な数量の組み合わせを示しています。Joséさんの場合は図6.2のようになります。JoséさんはTシャツを集めることと映画を見ることが好きです。
図6.2では横軸にTシャツの数量、縦軸に映画の本数を示しています。もしJoséさんの所得が無限である場合、あるいは財が無料である場合、Joséさんは際限なく財を消費することができます。しかし、Joséさんにも予算制約があります。Joséさんは56ドルを使うことができるとします。Tシャツの価格は14ドルで、映画の価格は7ドルです。この場合、予算制約線の縦軸との切片では8つの映画と0個のTシャツとなります(56ドル / 7ドル = 8)。予算制約線と横軸との切片では4つのTシャツと0本の映画となります(56ドル / 14ドル = 4)。予算制約線の傾きは –8 / 4= –2 となります。予算制約線上の選択は買うことのできるTシャツと映画の数量の組み合わせを示しています。
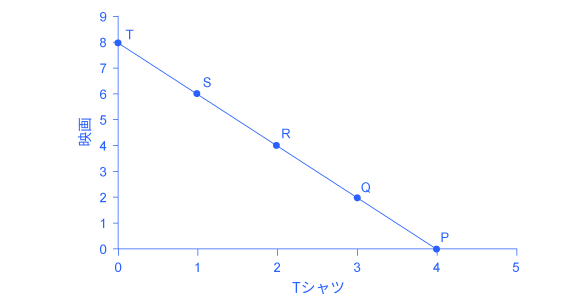
図6.2 消費材の選択Joséの所得は56ドルです。映画の料金は7ドル、Tシャツは14ドルです。予算制約線上の点は購入可能な映画とTシャツの価格の組み合わせを示します。
Joséは自分に最も大きい効用をもたらす財の数の組み合わせを選びたいと思っています。効用とは、経済学者が、ある人の選択がもたらすその人にとっての満足度や幸福度を表す用語です。
Joséが彼自身の効用を単位効用と呼ばれるものを利用して測定できるという仮定から始めましょう。この仮定については後ほど詳しく見ていきます。(ひとつ注意点として、個々の単位効用を比較することはできないということは覚えておきましょう。もし一人の人が一杯のコーヒーから20単位効用を得て、もう一人は10単位効用だったとしても、これは1人目の人がもう一人よりもより多くの楽しみを得たとか、コーヒーを2倍楽しんだといった意味ではありません。なぜかというと、単位効用は個々の主観に基づくからです。単位効用の測り方は人によって異なります。)表6.2はJoséの効用がどのように彼のTシャツと映画の消費に関係しているかを示しています。表の1列目はTシャツの消費量を示しています。2列目はJoséがTシャツを消費するにあたって得られる効用または満足度の合計を示しています。効用の合計における最も一般的なパターンは、追加で財を消費することはより大きい総効用につながりますが、その増加率は減少していく、というものです。3列目は追加で消費された財1単位によって新たに得られた効用である限界効用を表しています。限界効用についての式は:
$$ MU = \frac{総効用の変化}{数量の変化} $$
表を見ると、限界効用は財が追加で消費されるにつれ減少していくことがわかります。これは追加で消費された財によって追加でもたらされる効用は、その前に消費された財によってもたらされる効用よりも少ないということを意味しています。例えば、Joséが購入する一つ目のTシャツは彼のお気に入りで、彼はそのTシャツから22単位効用を得ます。Joséが購入する4つ目のTシャツは彼の他の衣服が全て洗濯されているときに着るような服で、そのTシャツは彼に18単位効用しか与えません。これらは財1単位の消費から追加で得られる効用は、その消費量が増えるに連れ減少するという限界効用逓減の法則の例です。限界効用逓減の法則は私たちが以前2.2章の「希少性の世界における選択」で学んだ、より包括的な「収穫逓減の法則」の一つの例です。
表6.2の残りはJoséの映画鑑賞数とそれらから得られる総効用と限界効用を表しています。Tシャツと同様に、総効用は映画の鑑賞回数とともに上昇します。限界効用もTシャツと同様に鑑賞回数が増えるにつれてその鑑賞から得られる効用は減少していきます。最初の映画鑑賞は彼がもっとも見たかったもので、彼に大きな効用または満足を与えます。5回目の映画鑑賞はただ単に時間をつぶすためのものかもしれません。総効用は限界効用の総和です。次のコラムを読んでそれらの計算方法を学びましょう。
| Tシャツ (数量) | 総効用 | 限界効用 | 映画 (数量) | 総効用 | 限界効用 |
|---|---|---|---|---|---|
| 1 | 22 | 22 | 1 | 16 | 16 |
| 2 | 43 | 21 | 2 | 31 | 15 |
| 3 | 63 | 20 | 3 | 45 | 14 |
| 4 | 81 | 18 | 4 | 58 | 13 |
| 5 | 97 | 16 | 5 | 70 | 12 |
| 6 | 111 | 14 | 6 | 81 | 11 |
| 7 | 123 | 12 | 7 | 91 | 10 |
| 8 | 133 | 10 | 8 | 100 | 9 |
表6.2 総効用と限界効用
表6.3は図6.2における予算制約線の5つの点に注目し、各Tシャツと映画の組み合わせにおけるJoséの総効用を計算しています。
| 点 | Tシャツ | 映画 | 総効用 |
|---|---|---|---|
| P | 4 | 0 | 81 + 0 = 81 |
| Q | 3 | 2 | 63 + 31 = 94 |
| R | 2 | 4 | 43 + 58 = 101 |
| S | 1 | 6 | 22 + 81 = 103 |
| T | 0 | 8 | 0 + 100 = 100 |
表6.3 最も効用の大きい選択の導出
総効用の計算
Joséがどのように選択をするのかをより詳細に見ていきましょう。
Step 1. (例として)Q点ではJoséは3枚のTシャツと2本の映画を消費しています。
Step 2. 表6.2を見てみましょう。4行2列目に3枚のTシャツは63 単位効用の価値があると書いてあります。同様に、2行5列目に2本の映画は31 単位効用の価値があると書いてあります。
Step 3. この情報から、Q点では総効用は94(63+31)であることが分かります。
Step 4. 表6.3のように、同じ計算をそれぞれの点について繰り返してみましょう。最後の列に総効用が示されています。
José にとって、S点において消費可能な財の組み合わせのうち最も総効用が最大になるのは、1枚のシャツと6本の映画を消費して得られる103単位効用です。
限界効用で選ぶ
ほとんどの人は少しづつ調節しながら、効用を最大化する組み合わせを見つけ出そうとします。この方法では、ある財の消費を増やしもう一方の消費を減らした時の限界効用によって測られる、トレードオフに注目しています。
例えば、初めにJosé は全てのお金をTシャツに注ぎ込むことを考えるとします。すなわち、図6.2の点Pのように、4枚のTシャツと0本の映画を消費する選択を考えます。そして、少ししか効用を生まないTシャツの消費を徐々に減らすことを考え、代わりに2本の映画を見ようと考えます。表6.4ではこの考えの一つ一つの段階を確認できます。次のコラムでは、限界効用が消費行動の選択にどのような影響を与え得るのかを説明します。
| 選択肢 | 選択肢の内容 | 総効用 | 一つ前の選択肢と比較した限界効用の変化 | 結論 |
|---|---|---|---|---|
| 選択肢1: P | Tシャツ4枚と映画0本 | Tシャツ4枚から81の単位効用 + 0本の映画から0の単位効用 = 81単位効用 | – | – |
| 選択肢2: Q | 3枚のTシャツと2本の映画 | Tシャツ3枚から63の単位効用 + 0本の映画から31の単位効用 = 94単位効用 | 1枚少ないTシャツから18単位効用の損失、2本の映画から31の単位効用、総効用は13の増加 | PよりもQが好ましい |
| 選択肢3: R | 2枚のTシャツと4本の映画 | Tシャツ2枚から43の単位効用 + 4本の映画から58の単位効用 = 101単位効用 | 1枚少ないTシャツから20単位効用の損失、2本の映画から27の単位効用、総効用は7の増加 | QよりもRが好ましい |
| 選択肢4: S | 1枚のTシャツと6本の映画 | Tシャツ1枚から22の単位効用 + 6本の映画から81の単位効用 = 103単位効用 | 1枚少ないTシャツから21単位効用の損失、2本の映画から23の単位効用、総効用は2の増加 | RよりもSが好ましい |
| 選択肢5: T | 0枚のTシャツと8本の映画 | Tシャツ0枚から0の単位効用 + 8本の映画から100の単位効用 = 100単位効用 | 1枚少ないTシャツから22単位効用の損失、2本の映画から19の単位効用、総効用は3の減少 | TよりもSが好ましい |
表6.4 効用最大化の工程
限界効用を比較し決定する
Joséさんは、(彼が単位効用を用いて考えるとすると)次のようなプロセスを用いることで購入するTシャツと映画のチケットの数を決定することができます。
ステップ1 表6.2でJoséさんが4枚目のTシャツ購入で得る効用は18単位効用です。もし、Joséさんが4枚目のTシャツの購入をやめた場合、彼は18の単位効用を失うことになります。
ステップ2 4枚目のTシャツの購入をやめると(Tシャツ1枚分の価格である)14ドルが自由に使えることになり、これでJoséさんは(それぞれ7ドルである)2つの映画を見ることが可能になります。
ステップ3 Joséさんは1つ目の映画の限界効用は16で、2つ目の映画の限界効用は15単位効用ということを知っています。そこで、もしJoséさんが点Pから点Qに移動すると考えると、彼は(Tシャツの購入量による)18の単位効用を諦めて(映画鑑賞による)31の単位効用を得ます。
ステップ4 31の単位効用を得て同時に18の単位効用を失ったということは結果的に13の単位効用を得たということになります。他の言い方だと点Qで得られる総効用(表6.3より94)は点P(81)で得られる全効用よりも13単位効用多いと言えます。
ステップ5 以上の過程からJoséさんは4つ目のTシャツの購入をやめて2つの映画を見ることを選択します。
Joséさんは明確に点Pより点Qを選ぶのが望ましいと考えます。では次に、この限界効用を用いた段階的な意思決定プロセスの段階的な過程を繰り返しましょう。Joséさんは追加で2枚の映画チケットを買う(27の限界効用を得る)ことと引き換えに、3枚目のTシャツを諦め(20の限界効用を諦め)ようと考えます。Joséさんは点Qより点Rを選びます。Joséさんが点Rより点Sを取るか考えるとどうなるでしょう。2枚目のTシャツを諦めることは21の限界効用を失うことを意味し、5回目と6回目の映画の限界効用は合わせて23となるでしょう。よってJoséさんは点Rより点Sを選びます。
しかしもしJoséさんが点Sより点Tを取ろうとすると、1枚目のTシャツを諦め22の限界効用を失いますが、追加の2回の映画からは合計19の限界効用しか得られないことが分かります。Joséさんが点Tを選んでいたら彼の限界効用は100単位効用へ落ちていたでしょう。これらのトレードオフの考えからJoséさんは、やはり1枚のTシャツと6回の映画の点Sが、最も高い総合効用をもたらす選択であると結論付けます。この段階的なアプローチから、Joséさんがどの点から考え始めても同じ結論にたどり着きます。
1ドルあたりの満足度に注目することによってこのアプローチをより機械的な方法にに発展させることができます。もしある商品が5ドルで10の単位効用をもたらすとすると、その商品は1ドルの支払いに対し2の単位効用を提供します。1ドルあたりの限界効用は、Joséさんが受け取った追加の効用の量を商品の価格で割ったものとなります。表6.5はJoséさんのTシャツと映画の1ドルあたりの限界効用を示しています。
$$ 1ドル当たりの限界効用 = \frac{限界効用}{価格} $$
もしJoséさんが限られた予算の中で最大の効用を得たいとするならば、彼は常に(予算が許す限り)1ドル当たりの限界効用が最大のものを購入するでしょう。Joséさんの選択は「何も購入していない」状態から始まります。もし彼がTシャツを購入した場合、1ドル当たりの効用は1.6単位効用となります。もし映画のチケットを購入した場合、1ドル当りの限界効用は2.3単位効用となります。このことから、Joséは最初に映画のチケットを購入するでしょう。なぜならば、それが購入可能な範囲で1ドル当りの限界効用が最大であるからです。次にJoséさんはまた映画のチケットを購入するでしょう。なぜならば2つ目の映画の限界効用(=2.14単位効用)は1枚目のTシャツの限界効用(=1.6単位効用)よりも大きいからです。Joséさんは予算が無くなるまで1ドル当りの限界効用が最大となる財を書い続けるとします。するとJoséさんは1ドル当りの効用が1枚目のTシャツと同じとなる6本目の映画まで、映画のチケットを購入し続けます。Joséさんは6本目の映画と1枚目のTシャツをちょうど購入するだけの予算があります。そのため最終的にJoséさんは6本の映画と1枚のTシャツを購入します。
| Tシャツの数兆 | 総効用 | 限界効用 | 1ドル当たりの限界効用 | 映画の数量 | 総効用 | 限界効用 | 1ドル当りの限界効用 |
|---|---|---|---|---|---|---|---|
| 1 | 22 | 22 | 22/$14=1.6 | 1 | 16 | 16 | 16/$7=2.3 |
| 2 | 43 | 21 | 21/$14=1.5 | 2 | 31 | 15 | 15/$7=2.14 |
| 3 | 63 | 20 | 20/$14=1.4 | 3 | 45 | 14 | 14/$7=2 |
| 4 | 81 | 18 | 18/$14=1.3 | 4 | 58 | 13 | 13/$7=1.9 |
| 5 | 97 | 16 | 16/$14=1.1 | 5 | 70 | 12 | 12/$7=1.7 |
| 6 | 111 | 14 | 14/$14=1 | 6 | 81 | 11 | 11/$7=1.6 |
| 7 | 123 | 12 | 12/$14=1.2 | 7 | 91 | 10 | 10/$7=1.4 |
表6.5 1ドル当りの限界効用
効用最大化の規則
意思決定の過程は効用を最大化するときに従うべきルールを示唆します。 Tシャツの価格は映画の価格の2倍なので、効用を最大化するためには、Joséさんが先ほど選んだTシャツは先ほどの映画の2倍の限界効用(以下の数式ではMU)を提供する必要があります。もし先ほどのTシャツの限界効用が映画で得られる効用の2倍よりも低ければ、同じ額を映画に使った時よりも1ドル当たりの限界効用が少ないことになります。そのような場合は、Joséさんが総効用を増やすためにTシャツを映画に差し替える必要があります。
もし最後に買うTシャツの限界効用が最後の映画に比べ2倍以上であれば、映画にそのお金を使うよりも、Tシャツの1ドル当たりの限界効用が大きくなります。結果としてJoséさんはより多くのTシャツを買うと考えられます。Joséさんの最適な選択は点Sの時で、Tシャツの限界効用は22であり、これは映画の限界効用である11のちょうど2倍であることが分かります。この場合1ドル当たりの限界効用は2つの財で同じです。これはJoséさんが効用が最大となる点を見つけていることを物語っています。
これは一般的に次のような法則をとります。もし常に1ドル当たりの限界効用が最大になるように商品を選び続ければ、予算が底をついた時点では、効用を最大化する選択は1ドル当たりの限界効用が2つの財で同じになるように行われるはずです。
$$ \frac{MU_1}{P_1} = \frac{MU_2}{P_2} $$
分別のある人であれば、2つの商品を比較してそれぞれから得られる効用が同じ場合、片方の商品に2倍の価格を支払うようなことはありません。上の表の数値の場合は下のようになります。
$$ \frac{22}{$14} = \frac{11}{$7} $$ $$ \therefore 1.6 = 1.6 $$
次のコラムではこの効用最大化の選択というコンセプトを順序立てて説明しています。
効用最大化
MU1/P1=MU2/P2 という一般的な法則は、それぞれの財において1ドル当たりの限界効用は全く同じであることを意味しています。今回で言うと点Sの場合です。
ステップ1:1ドルを追加で映画に出すことを1ドルを追加でTシャツに出すことに交換した場合、Tシャツから得られる限界効用は映画から得られたであろう限界効用でちょうど相殺されます。つまり純利益はゼロになります。
ステップ2:しかし、製品は大抵1ドル以上のコストがかかるため、1ドルの価値の映画と交換することはできません。できることは2つの映画を他のTシャツと交換することです。この例では、映画一本はTシャツ2枚分の価格です。
ステップ3:2つの映画をTシャツ1つと交換した場合、点Rになります。(Tシャツ2つと映画4つ)
ステップ4:表6.4の選択4から、点Rに移動したとき、追加の1枚のTシャツから21単位効用を得て、2つの映画から23単位効用を失うことがわかります。結果として、点Rでは総効用が減ることになります。
上記の一般的な法則は、消費者均衡と呼ばれる、効用最大化の選択示しています。
一般的な法則を、2つの財の価格の比率が限界効用の比率と一致している状態として表すことも可能です。財1の価格を財2の価格で割った値は、効用が最大となる点では財1の限界効用を財2の限界効用で割った値と一致します。
$$ \frac{P_1}{P_2} = \frac{MU_1}{MU_2} $$
予算制約上では2つの財の合計価格は一定なので、価格の比率は変化しません。しかし消費された数量に合わせて2つの財の限界効用は変化します。最適と考えられる点S、つまり1枚のTシャツと6本の映画を選択する点では、Tシャツの限界効用と価格の比率(22:14)は、映画の限界効用と価格の比率(11:7)と一致します。
数字で効用を計る
以上の効用の議論は、効用を数値として把握することが可能であるという仮定のもと行ってきました。しかしこの仮定ははたして現実的なのでしょうか。気温を測りたい場合は温度計を使えば良いですが、効用を測りたくても「効用計」なんてものは存在しません。効用の説明を明確にするためにこの仮定は便利ですが、この仮定での数値は第三者が知ることができるものではなく、選択を行う当人だけが2つの選択のどちらを好むかを考えるときにのみ知ることのできるものです。
これを理解するために、効用が最大となる選択を見つけるための段階的なプロセスを思い出しましょう。このプロセスでは、予算制約線上の複数の選択を考えるとき、ある選択から得られる限界効用と失う限界効用を比較しました。Joséが予算制約線上の選択を比較するとき、重要なのは効用を表す数字ではなく、彼が数字を使うかどうかでもなく、彼だけがどの選択を好むかがわかるということです。
このように、効用が最大となる選択肢を選ぶためのプロセスは多くの人が消費選択を行うかと非常に似ているといえます。私達が一番幸せになる選択が何であるか、ものの値段がどうであるか、何かを多く買うために何を諦めるべきかを私達は考えます。私達は、私達を最も満足させるものを選ぶのです。予算制約線、総効用、限界効用といった単語は日常のプロセスを明確で具体的な方法で説明するための道具にすぎません。「単位効用計測器」を探すことは不可能ですので、効用を表す数値は議論の中心ではないことは幸運と言えるでしょう。この章の最後までに、計測することのできない単位効用ではなく、計ることのできる需要を用いて分析が行えるようになります。
批判的思考のための問題
- 最近した買い物を思い出して、購入を決めるまでの思考の過程を考えてみましょう。
- 政治における決まり事は、経済学における決まりごととは必ずしも同じではありません。政府機関の予算を設定する際の議論では、「ワシントン記念塔の閉鎖」と呼ばれる戦略があります。ある機関の予算削減が検討されると、その機関は多くの人に親しまれている有名な観光地(例えばワシントン記念塔)を閉鎖することを決定することがあります。限界効用逓減の法則を用いて、この戦略がいかに的外れであるかを説明しましょう。(ヒント:もし予算削減という状況の中最大限の行動を取りたいなら、予算の中にある、限界効用が最大であるものを削ぎ落とすのが良いのでしょうか、それとも限界効用が最小であるものを削ぎ落とすのが良いのでしょうか。「ワシントン記念塔の閉鎖」戦略は限界効用が最大のものを削ぎ落とすのでしょうか、それとも最小のものを削ぎ落とすのでしょうか。)
対訳表
| 予算制約線 | budget constraint (or budget line) |
| 総効用 | total utility |
| 限界効用 | marginal utility |
| 限界効用逓減 | diminishing marginal utility |
| 1ドルあたりの限界効用 | marginal utility per dollar |
| 消費者均衡 | consumer equilibrium |